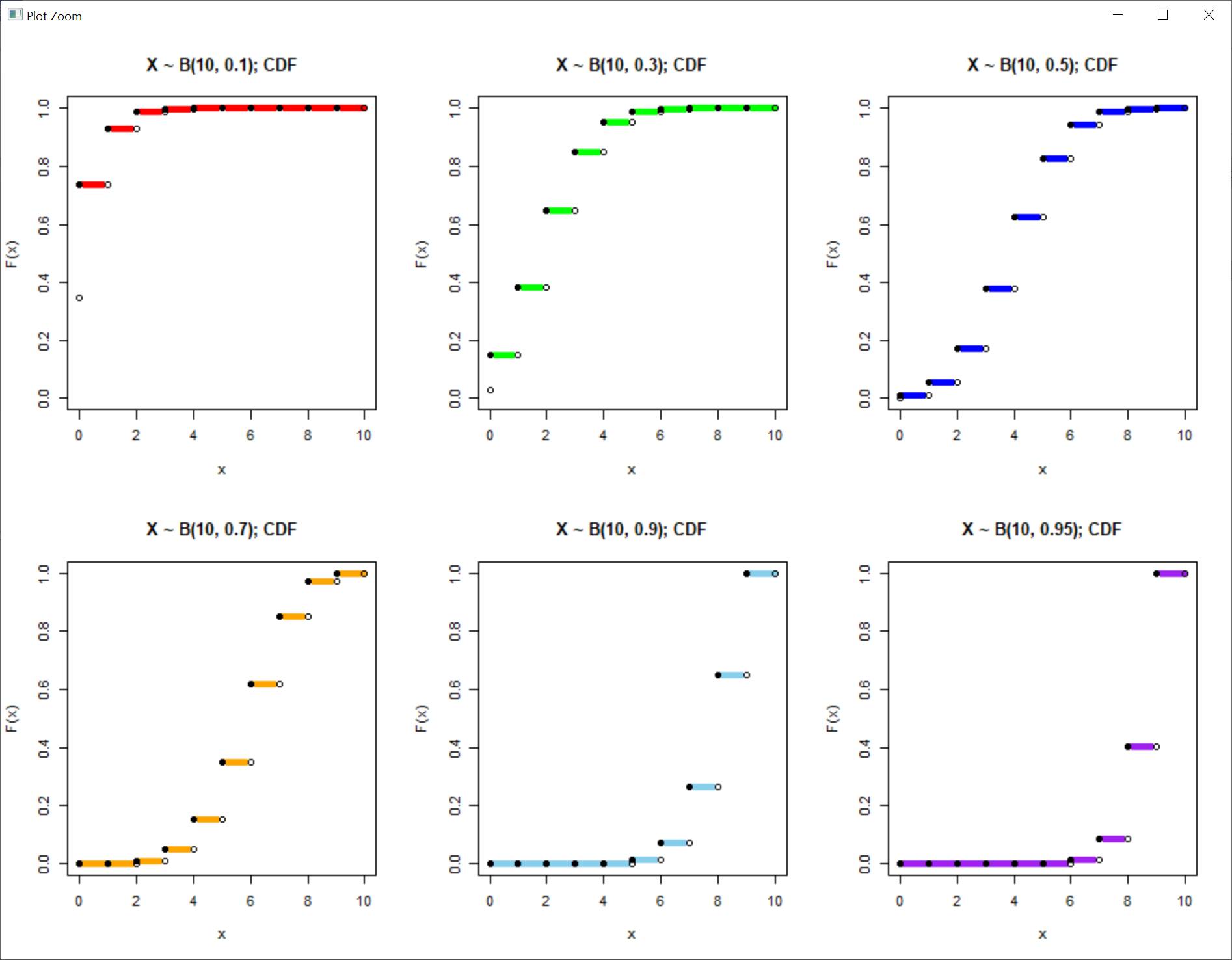
> ##### 실습2. 이항분포의 누적분포함수 #####
> opar <- par(mfrow=c(2,3)) # plot 영역을 행 우선으로 하여 2행 3열로 나눔
>
> p <- 0.1; n <- 10; x <- 0:10 # 확률 0.1, 시행횟수 10회일 때 0~10회 성공할 확률분포
> binom.pdf <- dbinom(0:n, size=n, prob=p) # 이항분포로 변수 생성
> cumsum(binom.pdf) # 누적확률분포 계산(1) = dbinom + cumsum
[1] 0.3486784 0.7360989 0.9298092 0.9872048 0.9983651 0.9998531 0.9999909 0.9999996
[9] 1.0000000 1.0000000 1.0000000
> (binom.cdf.1 <- cumsum(binom.pdf)) # 누적확률분포 값을 새 변수로 생성
[1] 0.3486784 0.7360989 0.9298092 0.9872048 0.9983651 0.9998531 0.9999909 0.9999996
[9] 1.0000000 1.0000000 1.0000000
> plot(x, binom.cdf.1, type='S', ylab='F(x)', xlab='x', ylim=c(0,1),
+ main="X ~ B(10, 0.1); CDF", lwd=5, col="Red", cex=2) # plot 생성
> points(x-1, binom.cdf.1, type='h', col="white", lwd=5) # type='h', col='white'로 하얀 세로막대선 생성, cdf에서 불필요한 y축 선을 하얀 선으로 덮는 효과 적용
> points(x-1, binom.cdf.1, pch=16) # 폐구간(시작점)
> points(x, binom.cdf.1, pch=1) # 개구간(종료점)
>
> # 확률을 0.3으로 변경
> p <- 0.3
> (binom.cdf.2 <- pbinom(0:n, size=n, prob=p)) # 누적확률분포 계산 (2)
[1] 0.02824752 0.14930835 0.38278279 0.64961072 0.84973167 0.95265101 0.98940792
[8] 0.99840961 0.99985631 0.99999410 1.00000000
> plot(x, binom.cdf.2, type='S', ylab='F(x)', xlab='x', ylim=c(0,1),
+ main="X ~ B(10, 0.3); CDF", lwd=5, col="Green", cex=2)
> points(x-1, binom.cdf.2, type='h', col="white", lwd=5)
> points(x-1, binom.cdf.2, pch=16)
> points(x, binom.cdf.2, pch=1)
>
> # 확률을 0.5으로 변경
> p <- 0.5
> (binom.cdf.3 <- pbinom(0:n, size=n, prob=p))
[1] 0.0009765625 0.0107421875 0.0546875000 0.1718750000 0.3769531250 0.6230468750
[7] 0.8281250000 0.9453125000 0.9892578125 0.9990234375 1.0000000000
> plot(x, binom.cdf.3, type='S', ylab='F(x)', xlab='x', ylim=c(0,1),
+ main="X ~ B(10, 0.5); CDF", lwd=5, col="Blue", cex=2)
> points(x-1, binom.cdf.3, type='h', col="white", lwd=5)
> points(x-1, binom.cdf.3, pch=16)
> points(x, binom.cdf.3, pch=1)
>
> # 확률을 0.7로 변경하여 실행
> p <- 0.7
> (binom.cdf.4 <- pbinom(0:n, size=n, prob=p))
[1] 0.0000059049 0.0001436859 0.0015903864 0.0105920784 0.0473489874 0.1502683326
[7] 0.3503892816 0.6172172136 0.8506916541 0.9717524751 1.0000000000
> plot(x, binom.cdf.4, type='S', ylab='F(x)', xlab='x', ylim=c(0,1),
+ main="X ~ B(10, 0.7); CDF", lwd=5, col="Orange", cex=2)
> points(x-1, binom.cdf.4, type='h', col="white", lwd=5)
> points(x-1, binom.cdf.4, pch=16)
> points(x, binom.cdf.4, pch=1)
>
> # 확률을 0.9로 변경하여 실행
> p <- 0.9
> (binom.cdf.5 <- pbinom(0:n, size=n, prob=p))
[1] 0.0000000001 0.0000000091 0.0000003736 0.0000091216 0.0001469026 0.0016349374
[7] 0.0127951984 0.0701908264 0.2639010709 0.6513215599 1.0000000000
> plot(x, binom.cdf.5, type='S', ylab='F(x)', xlab='x', ylim=c(0,1),
+ main="X ~ B(10, 0.9); CDF", lwd=5, col="Skyblue", cex=2)
> points(x-1, binom.cdf.5, type='h', col="white", lwd=5)
> points(x-1, binom.cdf.5, pch=16)
> points(x, binom.cdf.5, pch=1)
>
> # 확률을 0.95로 변경하여 실행
> p <- 0.95
> (binom.cdf.6 <- pbinom(0:n, size=n, prob=p))
[1] 9.765625e-14 1.865234e-11 1.605078e-09 8.198398e-08 2.754583e-06 6.368983e-05
[7] 1.028498e-03 1.150356e-02 8.613836e-02 4.012631e-01 1.000000e+00
> plot(x, binom.cdf.6, type='S', ylab='F(x)', xlab='x', ylim=c(0,1),
+ main="X ~ B(10, 0.95); CDF", lwd=5, col="Purple", cex=2)
> points(x-1, binom.cdf.6, type='h', col="white", lwd=5)
> points(x-1, binom.cdf.6, pch=16)
> points(x, binom.cdf.6, pch=1)
>
> # plot을 원래의 형태(mfrow=c(1,1))로 복원
> par(opar)
'데이터 [Data] > R' 카테고리의 다른 글
| R Distributions: 초기하분포, 초기하분포의 이항근사 (0) | 2021.06.07 |
|---|---|
| R Distributions: 포아송분포 (0) | 2021.06.06 |
| R Distributions: 이항분포 (0) | 2021.06.04 |
| R Graphics 3: 문자나 점의 크기, 그래픽모수, 플랏영역, 좌표축범위 (0) | 2021.06.03 |
| R Graphics 2: 그래프유형, 색상, 낮은 수준의 그래프함수 (0) | 2021.06.02 |




댓글