> # 2) 초기하분포의 누적분포함수
>
> # 초기값으로 재설정
> N <- 20; K <- 4; p <- 0.2
>
> # plot 영역을 행 우선으로 하여 2행 3열로 나눔 (모수 N을 6개 사용)
> chpar <- par(mfrow=c(2,3))
>
> # phyper() 함수를 이용하여 초기하분포의 cdf 변수인 c.hyper 생성
> c.hyper1 <- phyper(x, K, N-K, n)
> # c.hyper의 plot 생성 : 누적확률분포이므로 y의 범위는 0부터 1까지로 지정
> plot(0:5, c.hyper1, type='S', col='Red', ylab='F(x)', xlab='X', lwd=3, ylim=c(0, 1),
+ main = c("X ~ HG(N=20; n=5, p=0.2); cdf"))
> # 하얀 배경에 하얀 선을 삽입하여 세로선을 가리는 효과 적용
> points(x-1, c.hyper1, type='h', col="white", lwd=5)
> # 폐구간(시작점)
> points(x-1, c.hyper1, pch=16)
> # 개구간(종료점)
> points(x, c.hyper1, pch=1)
>
> # 모수 N을 각각 30, 50, 100, 500, 1000으로 각각 변경하며,
> # 고정된 p값(0.2)를 이용하여 K도 변경(6, 10, 20, 100, 200) 후 위 과정 반복
> # c.hyper 변수와 이에 따른 각각의 cdf plot 생성
> N <- 30; K <- N*p; c.hyper2 <- phyper(x, K, N-K, n)
> plot(0:5, c.hyper2, type='S', col='Green', ylab='F(x)', xlab='X', lwd=3, ylim=c(0, 1),
+ main = c("X ~ HG(N=30; n=5, p=0.2); cdf"))
> points(x-1, c.hyper2, type='h', col="white", lwd=5)
> points(x-1, c.hyper2, pch=16)
> points(x, c.hyper2, pch=1)
>
> N <- 50; K <- N*p; c.hyper3 <- phyper(x, K, N-K, n)
> plot(0:5, c.hyper3, type='S', col='Blue', ylab='F(x)', xlab='X', lwd=3, ylim=c(0, 1),
+ main = c("X ~ HG(N=50; n=5, p=0.2); cdf"))
> points(x-1, c.hyper3, type='h', col="white", lwd=5)
> points(x-1, c.hyper3, pch=16)
> points(x, c.hyper3, pch=1)
>
> N <- 100; K <- N*p; c.hyper4 <- phyper(x, K, N-K, n)
> plot(0:5, c.hyper4, type='S', col='Orange', ylab='F(x)', xlab='X', lwd=3, ylim=c(0, 1),
+ main = c("X ~ HG(N=100; n=5, p=0.2); cdf"))
> points(x-1, c.hyper4, type='h', col="white", lwd=5)
> points(x-1, c.hyper4, pch=16)
> points(x, c.hyper4, pch=1)
>
> N <- 500; K <- N*p; c.hyper5 <- phyper(x, K, N-K, n)
> plot(0:5, c.hyper5, type='S', col='Skyblue', ylab='F(x)', xlab='X', lwd=3, ylim=c(0, 1),
+ main = c("X ~ HG(N=500; n=5, p=0.2); cdf"))
> points(x-1, c.hyper5, type='h', col="white", lwd=5)
> points(x-1, c.hyper5, pch=16)
> points(x, c.hyper5, pch=1)
>
> N <- 1000; K <- N*p; c.hyper6 <- phyper(x, K, N-K, n)
> plot(0:5, c.hyper6, type='S', col='Purple', ylab='F(x)', xlab='X', lwd=3, ylim=c(0, 1),
+ main = c("X ~ HG(N=1000; n=5, p=0.2); cdf"))
> points(x-1, c.hyper6, type='h', col="white", lwd=5)
> points(x-1, c.hyper6, pch=16)
> points(x, c.hyper6, pch=1)
>
> # plot의 영역을 원래의 형태(mfrow=c(1,1))로 복원
> par(chpar)

> # 4) 이항분포의 누적분포함수
>
> # plot 영역을 행 우선으로 하여 3행 5열로 나눔 (모수 n을 3개 * p를 5개 사용)
> # 모수 n = 20, 30, 50; p = 0.2, 0.3, 0.5, 0.7, 0.8을 사용할 예정
> cbpar <- par(mfrow=c(3,5))
>
> # 초기값 설정: n=20, p=0.2, x=0:20
> p <- 0.2; n <- 20; x <- 0:20
> # n=20, p=0.2일 때 이항분포의 cdf 변수 및 plot 생성
> c.binom11 <- pbinom(0:n, size=n, prob=p)
> plot(x, c.binom11, type='S', ylab='F(x)', xlab='X', ylim=c(0,1),
+ main="X ~ B(20, 0.2); cdf", lwd=5, col="Red", cex=2)
> # 하얀 배경에 하얀 선을 삽입하여 세로선을 가리는 효과 적용
> points(x-1, c.binom11, type='h', col="white", lwd=5)
> # 폐구간(시작점)
> points(x-1, c.binom11, pch=16)
> # 개구간(종료점)
> points(x, c.binom11, pch=1)
>
> # n=20일 때, p를 0.3으로 변경
> p <- 0.3
> # 위 과정을 반복하여 c.binom 변수와 이에 따른 각각의 cdf plot 생성
> c.binom12 <- pbinom(0:n, size=n, prob=p)
> plot(x, c.binom12, type='S', ylab='F(x)', xlab='X', ylim=c(0,1),
+ main="X ~ B(20, 0.3); cdf", lwd=5, col="Orange", cex=2)
> points(x-1, c.binom12, type='h', col="white", lwd=5)
> points(x-1, c.binom12, pch=16)
> points(x, c.binom12, pch=1)
>
> # n=20일 때, p를 0.5로 변경
> p <- 0.5
> c.binom13 <- pbinom(0:n, size=n, prob=p)
> plot(x, c.binom13, type='S', ylab='F(x)', xlab='X', ylim=c(0,1),
+ main="X ~ B(20, 0.5); cdf", lwd=5, col="Yellow", cex=2)
> points(x-1, c.binom13, type='h', col="white", lwd=5)
> points(x-1, c.binom13, pch=16)
> points(x, c.binom13, pch=1)
>
> # n=20일 때, p를 0.7로 변경
> p <- 0.7
> c.binom14 <- pbinom(0:n, size=n, prob=p)
> plot(x, c.binom14, type='S', ylab='F(x)', xlab='X', ylim=c(0,1),
+ main="X ~ B(20, 0.7); cdf", lwd=5, col="Green", cex=2)
> points(x-1, c.binom14, type='h', col="white", lwd=5)
> points(x-1, c.binom14, pch=16)
> points(x, c.binom14, pch=1)
>
> # n=20일 때, p를 0.8로 변경
> p <- 0.8
> c.binom15 <- pbinom(0:n, size=n, prob=p)
> plot(x, c.binom15, type='S', ylab='F(x)', xlab='X', ylim=c(0,1),
+ main="X ~ B(20, 0.8); cdf", lwd=5, col="Blue", cex=2)
> points(x-1, c.binom15, type='h', col="white", lwd=5)
> points(x-1, c.binom15, pch=16)
> points(x, c.binom15, pch=1)
>
> # n=30, p=0.2로 변경하며, x = 0:n이므로 x는 0부터 30까지로 변경
> p <- 0.2; n <- 30; x <- 0:30
> c.binom21 <- pbinom(0:n, size=n, prob=p)
> plot(x, c.binom21, type='S', ylab='F(x)', xlab='X', ylim=c(0,1),
+ main="X ~ B(30, 0.2); cdf", lwd=5, col="Red", cex=2)
> points(x-1, c.binom21, type='h', col="white", lwd=5)
> points(x-1, c.binom21, pch=16)
> points(x, c.binom21, pch=1)
>
> # n=30일 때, p를 0.3으로 변경
> p <- 0.3
> c.binom22 <- pbinom(0:n, size=n, prob=p)
> plot(x, c.binom22, type='S', ylab='F(x)', xlab='X', ylim=c(0,1),
+ main="X ~ B(30, 0.3); cdf", lwd=5, col="Orange", cex=2)
> points(x-1, c.binom22, type='h', col="white", lwd=5)
> points(x-1, c.binom22, pch=16)
> points(x, c.binom22, pch=1)
>
> # n=30일 때, p를 0.5로 변경
> p <- 0.5
> c.binom23 <- pbinom(0:n, size=n, prob=p)
> plot(x, c.binom23, type='S', ylab='F(x)', xlab='X', ylim=c(0,1),
+ main="X ~ B(30, 0.5); cdf", lwd=5, col="Yellow", cex=2)
> points(x-1, c.binom23, type='h', col="white", lwd=5)
> points(x-1, c.binom23, pch=16)
> points(x, c.binom23, pch=1)
>
> # n=30일 때, p를 0.7로 변경
> p <- 0.7
> c.binom24 <- pbinom(0:n, size=n, prob=p)
> plot(x, c.binom24, type='S', ylab='F(x)', xlab='X', ylim=c(0,1),
+ main="X ~ B(30, 0.7); cdf", lwd=5, col="Green", cex=2)
> points(x-1, c.binom24, type='h', col="white", lwd=5)
> points(x-1, c.binom24, pch=16)
> points(x, c.binom24, pch=1)
>
> # n=30일 때, p를 0.8로 변경
> p <- 0.8
> c.binom25 <- pbinom(0:n, size=n, prob=p)
> plot(x, c.binom25, type='S', ylab='F(x)', xlab='X', ylim=c(0,1),
+ main="X ~ B(30, 0.8); cdf", lwd=5, col="Blue", cex=2)
> points(x-1, c.binom25, type='h', col="white", lwd=5)
> points(x-1, c.binom25, pch=16)
> points(x, c.binom25, pch=1)
>
> # n=50, p=0.2로 변경하며, x = 0:n이므로 x는 0부터 50까지로 변경
> p <- 0.2; n <- 50; x <- 0:50
> c.binom31 <- pbinom(0:n, size=n, prob=p)
> plot(x, c.binom31, type='S', ylab='F(x)', xlab='X', ylim=c(0,1),
+ main="X ~ B(50, 0.2); cdf", lwd=5, col="Red", cex=2)
> points(x-1, c.binom31, type='h', col="white", lwd=5)
> points(x-1, c.binom31, pch=16)
> points(x, c.binom31, pch=1)
>
> # n=50일 때, p를 0.3으로 변경
> p <- 0.3
> c.binom32 <- pbinom(0:n, size=n, prob=p)
> plot(x, c.binom32, type='S', ylab='F(x)', xlab='X', ylim=c(0,1),
+ main="X ~ B(50, 0.3); cdf", lwd=5, col="Orange", cex=2)
> points(x-1, c.binom32, type='h', col="white", lwd=5)
> points(x-1, c.binom32, pch=16)
> points(x, c.binom32, pch=1)
>
> # n=50일 때, p를 0.5로 변경
> p <- 0.5
> c.binom33 <- pbinom(0:n, size=n, prob=p)
> plot(x, c.binom33, type='S', ylab='F(x)', xlab='X', ylim=c(0,1),
+ main="X ~ B(50, 0.5); cdf", lwd=5, col="Yellow", cex=2)
> points(x-1, c.binom33, type='h', col="white", lwd=5)
> points(x-1, c.binom33, pch=16)
> points(x, c.binom33, pch=1)
>
> # n=50일 때, p를 0.7로 변경
> p <- 0.7
> c.binom34 <- pbinom(0:n, size=n, prob=p)
> plot(x, c.binom34, type='S', ylab='F(x)', xlab='X', ylim=c(0,1),
+ main="X ~ B(50, 0.7); cdf", lwd=5, col="Green", cex=2)
> points(x-1, c.binom34, type='h', col="white", lwd=5)
> points(x-1, c.binom34, pch=16)
> points(x, c.binom34, pch=1)
>
> # n=50일 때, p를 0.8로 변경
> p <- 0.8
> c.binom35 <- pbinom(0:n, size=n, prob=p)
> plot(x, c.binom35, type='S', ylab='F(x)', xlab='X', ylim=c(0,1),
+ main="X ~ B(50, 0.8); cdf", lwd=5, col="Blue", cex=2)
> points(x-1, c.binom35, type='h', col="white", lwd=5)
> points(x-1, c.binom35, pch=16)
> points(x, c.binom35, pch=1)
>
> # plot을 원래의 형태(mfrow=c(1,1))로 복원
> par(cbpar)
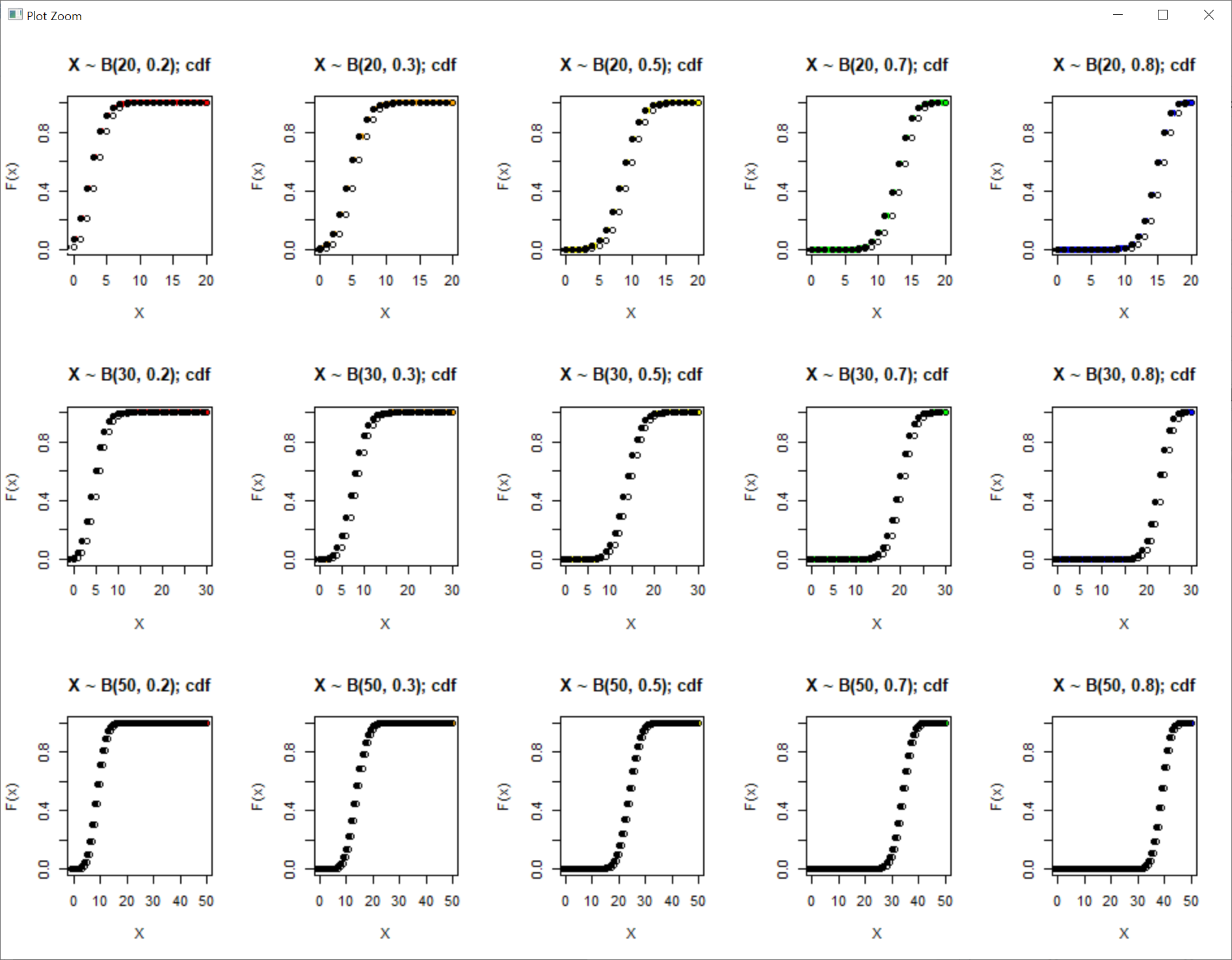
> # 4-2) 알고리즘을 활용한 이항분포의 cdf
> opar <- par(mfrow=c(3,5))
> n <- c(20, 30, 50)
> p <- c(0.2, 0.3, 0.5, 0.7, 0.8)
> for(i in 1:3){
+ for(j in 1:5){
+ x <- 0:n[i]
+ plot(x, p.binom <- pbinom(x, n[i], p[j]), type='S', xlab='X', ylab="", ylim=c(0, 1))
+ points(x-1, p.binom, type='h', col="white", lwd=5)
+ points(x-1, p.binom, pch=16)
+ points(x, p.binom, pch=1)
+ mtext(paste0("X~", "B(", n[i], ", ", p[j], ")"))
+ }
+ }
> par(opar)

> # 6) 포아송분포의 누적분포함수
>
> # plot 영역을 행 우선으로 하여 2행 4열로 나눔 (모수 lambda=n*p를 8개 사용)
> cppar <- par(mfrow=c(2,4))
>
> # n*p를 6까지 지정할 예정이므로 x를 0부터 15까지로 지정
> n <- 15; x <- 0:15
>
> # lambda=n*p=0.5부터 6까지, x=0:15 일 때 포아송분포의 cdf 변수 및 plot 생성
> # col(색상)은 고유번호로 지정, 1부터 8까지 순환하는 구조이므로 모수 n*p를 8개까지 사용
> # 누적확률분포이므로 y의 범위는 0부터 1까지로 지정
>
> # 포아송분포의 cdf 변수 p.pois의 순서 번호는 모수 lambda에 맞춰 지정
> # n*p=lambda=0.5일 때의 포아송분포 cdf 변수(c.pois0.5)와 plot 생성
> c.pois0.5 <- ppois(0:n, 0.5)
> plot(x, c.pois0.5, type='S', ylab='F(x)', xlab='x', ylim=c(0,1),
+ main="X ~ Poisson(0.5); cdf", lwd=5, col=1)
> # 하얀 배경에 하얀 선을 삽입하여 세로선을 가리는 효과 적용
> points(x-1, c.pois0.5, type='h', col="white", lwd=5)
> # 폐구간(시작점)
> points(x-1, c.pois0.5, pch=16)
> # 개구간(종료점)
> points(x, c.pois0.5, pch=1)
>
> # n*p=lambda=1일 때의 포아송분포 cdf 변수(c.pois1)와 plot 생성
> c.pois1 <- ppois(0:n, 1)
> plot(x, c.pois1, type='S', ylab='F(x)', xlab='x', ylim=c(0,1),
+ main="X ~ Poisson(1); cdf", lwd=5, col=2)
> # 세로선 가린 후, 폐구간과 개구간 표현
> points(x-1, c.pois1, type='h', col="white", lwd=5)
> points(x-1, c.pois1, pch=16)
> points(x, c.pois1, pch=1)
>
> # n*p=lambda=1.5일 때의 포아송분포 cdf 변수(c.pois1.5)와 plot 생성
> c.pois1.5 <- ppois(0:n, 1.5)
> plot(x, c.pois1.5, type='S', ylab='F(x)', xlab='x', ylim=c(0,1),
+ main="X ~ Poisson(1.5); cdf", lwd=5, col=3)
> # 세로선 가린 후, 폐구간과 개구간 표현
> points(x-1, c.pois1.5, type='h', col="white", lwd=5)
> points(x-1, c.pois1.5, pch=16)
> points(x, c.pois1.5, pch=1)
>
> # n*p=lambda=2일 때의 포아송분포 cdf 변수(c.pois2)와 plot 생성
> c.pois2 <- ppois(0:n, 2)
> plot(x, c.pois2, type='S', ylab='F(x)', xlab='x', ylim=c(0,1),
+ main="X ~ Poisson(2); cdf", lwd=5, col=4)
> # 세로선 가린 후, 폐구간과 개구간 표현
> points(x-1, c.pois2, type='h', col="white", lwd=5)
> points(x-1, c.pois2, pch=16)
> points(x, c.pois2, pch=1)
>
> # n*p=lambda=3일 때의 포아송분포 cdf 변수(c.pois3)와 plot 생성
> c.pois3 <- ppois(0:n, 3)
> plot(x, c.pois3, type='S', ylab='F(x)', xlab='x', ylim=c(0,1),
+ main="X ~ Poisson(3); cdf", lwd=5, col=5)
> # 세로선 가린 후, 폐구간과 개구간 표현
> points(x-1, c.pois3, type='h', col="white", lwd=5)
> points(x-1, c.pois3, pch=16)
> points(x, c.pois3, pch=1)
>
> # n*p=lambda=4일 때의 포아송분포 cdf 변수(c.pois4)와 plot 생성
> c.pois4 <- ppois(0:n, 4)
> plot(x, c.pois4, type='S', ylab='F(x)', xlab='x', ylim=c(0,1),
+ main="X ~ Poisson(4); cdf", lwd=5, col=6)
> # 세로선 가린 후, 폐구간과 개구간 표현
> points(x-1, c.pois4, type='h', col="white", lwd=5)
> points(x-1, c.pois4, pch=16)
> points(x, c.pois4, pch=1)
>
> # n*p=lambda=5일 때의 포아송분포 cdf 변수(c.pois5)와 plot 생성
> c.pois5 <- ppois(0:n, 5)
> plot(x, c.pois5, type='S', ylab='F(x)', xlab='x', ylim=c(0,1),
+ main="X ~ Poisson(5); cdf", lwd=5, col=7)
> # 세로선 가린 후, 폐구간과 개구간 표현
> points(x-1, c.pois5, type='h', col="white", lwd=5)
> points(x-1, c.pois5, pch=16)
> points(x, c.pois5, pch=1)
>
> # n*p=lambda=6일 때의 포아송분포 cdf 변수(c.pois6)와 plot 생성
> c.pois6 <- ppois(0:n, 6)
> plot(x, c.pois6, type='S', ylab='F(x)', xlab='x', ylim=c(0,1),
+ main="X ~ Poisson(6); cdf", lwd=5, col=8)
> # 세로선 가린 후, 폐구간과 개구간 표현
> points(x-1, c.pois6, type='h', col="white", lwd=5)
> points(x-1, c.pois6, pch=16)
> points(x, c.pois6, pch=1)
>
> # plot을 원래의 형태(mfrow=c(1,1))로 복원
> par(cppar)

'데이터 [Data] > R' 카테고리의 다른 글
| R 데이터시각화 함수를 활용한 탐색적 자료분석 (0) | 2021.06.10 |
|---|---|
| R plot: 이산형 분포의 근사 (0) | 2021.06.09 |
| R plot: 이산형 분포의 확률밀도함수 (0) | 2021.06.08 |
| 워드클라우드 자체실습: wordcloud2() (0) | 2021.06.07 |
| R Distributions: 초기하분포, 초기하분포의 이항근사 (0) | 2021.06.07 |




댓글